Etage d'entrÃĐe d'un amplificateur professionnel
- DÃĐtails
- CatÃĐgorie : Travaux dirigÃĐs d'ÃĐlectronique analogique
Pour que vos rÃĐsultats soient conservÃĐs, il est nÃĐcessaire de vous inscrire sur le site et de vous authentifier.
Ce problÃĻme propose l'ÃĐtude des ÃĐtages d'entrÃĐe et de traitement du signal d'un amplificateur Yamaha P3500S qui constitue l'entrÃĐe de gamme des amplificateurs de sonorisation professionnelle du constructeur. Tous les schÃĐmas prÃĐsentÃĐs dans ce problÃĻme sont tirÃĐs du Service Manual des Yamaha P1000S à P3500S et sont la propriÃĐtÃĐ de Yamaha. Ils sont proposÃĐs ici à des fins pÃĐdagoqiques.
PrÃĐsentation gÃĐnÃĐrale
Les caractÃĐristiques des amplificateurs de la sÃĐrie P1000S Ã P3500S sont indiquÃĐes :

Le synoptique de l'amplificateur est le suivant :

Dans l'ÃĐtude qui suit, on ne s'intÃĐresse qu'à la partie prÃĐsentÃĐe en haut à gauche sur le synoptique gÃĐnÃĐral et intitulÃĐe SUB(VR) dont un agrandissement sera proposÃĐ au moment de l'ÃĐtude.
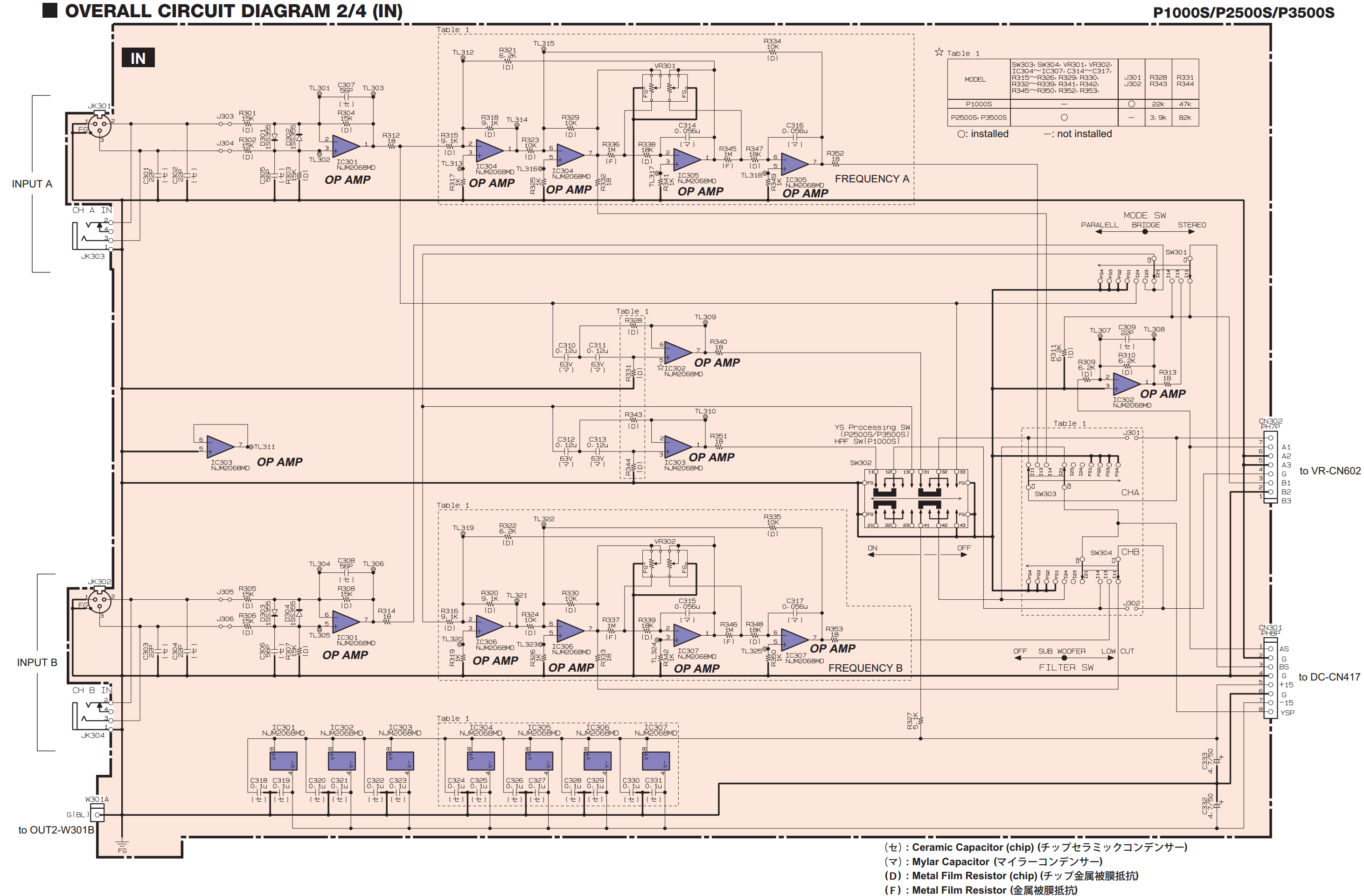
Pour finir, la figure ci-dessous prÃĐsente le schÃĐma complet du bloc d'entrÃĐes et de son traitement du signal analogique (cliquer dessous pour l'ouvrir en haute rÃĐsolution). On remarquera que ces ÃĐtages font la part belle aux amplificateurs opÃĐrationnels, tous produits par Yamaha.
Etude gÃĐnÃĐrale
L'ÃĐtude est rÃĐalisÃĐe en considÃĐrant les amplificateurs opÃĐrationnels comme parfaits.
1. Etude gÃĐnÃĐrale : synoptique des circuits d'entrÃĐes
1.1. Quelques dÃĐtails sur ce synoptique en se limitant au canal A :
- L'entrÃĐe est symÃĐtrique et se fait soit sur un connecteur Jack 6.35 (JK303), soit sur un connecteur XLR (JK301).
Remarque : â SymÃĐtrique â signifie que l'entrÃĐe se fait sur 3 points de connection : la masse (borne 1), le + (borne 3) appelÃĐ ÃĐgalement point chaud, le - (borne 2) dÃĐnommÃĐ aussi point froid. Le potentiel du point chaud est opposÃĐ au potentiel du point froid (on dit qu'ils sont en opposition de phase). - Le bloc BA permet de dÃĐssymÃĐtriser le signal d'entrÃĐe (voir ÃĐtude par la suite).
- Le signal peut ensuite Être traitÃĐ de diffÃĐrentes façons en fonction des besoins (sÃĐlection rÃĐalisÃĐe par les commutateurs SW302 et SW303):
- Filtrage via le bloc State Variable Active Filter (ÃĐtude dans la suite du sujet),
- Correction active avec le bloc YSP spÃĐcifique aux enceintes de sonorisation Yamaha.
- Le switch SW301 permet de choisir entre trois modes de fonctionnement de l'amplificateur : STEREO, PARALLEL, BRIDGE.
- Le signal peut ensuite Être attÃĐnuÃĐ avec le potentiomÃĻtre VR601 prÃĐsent en façade de l'amplificateur.
- A la sortie du potentiomÃĻtre VR601, on trouve une dÃĐrivation vers un amplificateur inverseur utilisÃĐ pour le fonctionnement de l'amplificateur en mode BRIDGE.
1.2. ComplÃĐment d'ÃĐtude sur le synoptique : modes de fonctionnement de l'amplificateur.
- En observant le trajet des signaux issus des canaux A et B, expliquer l'utilitÃĐ du mode PARALLEL.
- MÊme question en ce qui concerne le mode BRIDGE.
Remarque : une bonne mÃĐthode pour comprendre ce qui se passe consiste à reprÃĐsenter une pÃĐriode de sinus sur le signal en sortie du bloc BA et de voir ce qu'on obtient sur les bornes de sorties de l'amplificateur.
DÃĐsymÃĐtrisation des entrÃĐes
2. Etude de l'ÃĐtage d'entrÃĐe de l'amplificateur ("dÃĐ-symÃĐtriseur")
Pour mÃĐmoire, le schÃĐma ÃĐlectronique complet correspondant au synoptique ÃĐtudiÃĐ Ã la question prÃĐcÃĐdente est disponible à la fin du texte prÃĐsentÃĐ sous l'onglet PrÃĐsentation gÃĐnÃĐrale.
On s'intÃĐresse ici au premier ÃĐtage de traitement des entrÃĐes dont la figure ci-dessous propose un zoom :
Cette figure correspond prÃĐcisÃĐment à celle que l'on trouve dans la manuel de service de l'amplificateur. Comme souvent lorsqu'on ÃĐtudie un circuit ÃĐlectronique, il peut Être judicieux de rÃĐamÃĐnager le circuit et de modifier les noms des composants pour des calculs plus lisibles. En particulier, on aura soin de noter identiquement les composants de valeurs ÃĐgales dÃĻs lors que l'ÃĐtude ne portera pas sur l'incidence de la tolÃĐrance des rÃĐsistances.
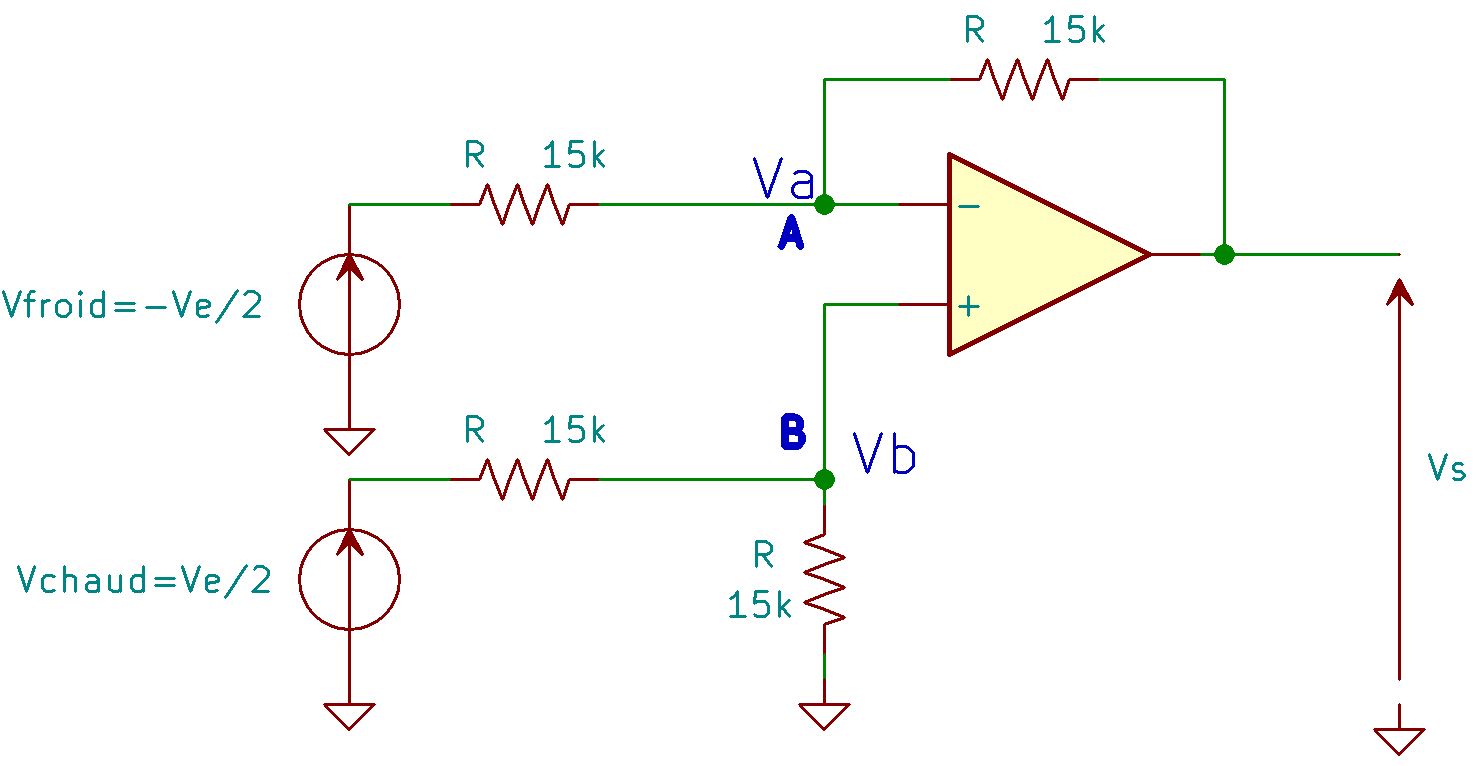
La figure remaniÃĐe pour les besoins de notre ÃĐtude est alors la suivante :

ConsidÃĐrons au niveau de l'entrÃĐe : \(V_{chaud}=-V_{froid}=\frac{V_{e}}{2}\) et le signal de sortie de ce premier ÃĐtage notÃĐ $V_{s}$.
- Sans faire d'ÃĐtude trÃĻs dÃĐtaillÃĐe, quelle sera l'action des capacitÃĐs $C_e$ ? En quoi sont-elles utiles ?
-
1
-
2
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- UtilitÃĐ des diodes D301 et D302 :
- L'amplificateur opÃĐrationnel IC301 fonctionne-t-il en linÃĐaire ou en non-linÃĐaire ? Quelle fonction rÃĐalise-t-il ? (sans faire de calcul)
-
1
-
2
-
3
-
4
-
5
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- Que peut-on en dÃĐduire quant à l'ÃĐtat des diodes D301 et D302 en fonctionnement normal ?
-
1
-
2
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- A quelle condition peuvent-elles changer d'ÃĐtat ?
-
1
-
2
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- En dÃĐduire en quoi elles sont utiles.
-
1
-
2
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- Quelle est l'utilitÃĐ de la rÃĐsistance de sortie $R_p$ ?
-
1
-
2
- Bonne rÃĐponse : 2 pt(s). Mauvaise rÃĐponse : -1 pt(s). Pas de rÃĐponse : 0 pt
- CaractÃĐristique entrÃĐe/sortie : approche simplifiÃĐe
Un calcul rapide de la frÃĐquence d'action des couples $R.C$ fournit la valeur $f=\frac1{2.\pi.R.C}=189kHz$ donc trÃĻs au delà de la bande audio. En premiÃĻre approximation, on peut donc se contenter d'ÃĐtudier le circuit suivant en supprimant les capacitÃĐs :
L'utilisation du thÃĐorÃĻme de Millman aux admittances justifie ce petit rappel :

ThÃĐorÃĻme de Millman Le thÃĐorÃĻme de Millman est la conjugaison de la loi des branches et de la lois des noeuds.
On considÃĻre N branches en parallÃĻles. Chaque branche est un gÃĐnÃĐrateur de ThÃĐvenin rÃĐsultant de la mise en sÃĐrie d'un gÃĐnÃĐrateur de tension et d'une impÃĐdance sÃĐrie. Pour la branche $i$, on note $V_i$ la tension du gÃĐnÃĐrateur ÃĐquivalent de ThÃĐvenin et $Z_i$ l'impÃĐdance de ce mÊme gÃĐnÃĐrateur. La diffÃĐrence de potentiels aux bornes des N branches s'ÃĐcrit alors $$\Large U_{AB} = \frac{ \sum\limits_{i=1}^n \frac{V_i}{Z_i}}{\sum\limits_{i=1}^n \frac1{Z_i}}$$. On peut ÃĐgalement l'ÃĐcrire à partir des admittances $Y_i=\frac{1}{Z_i}$ et il vient alors : $$\Large U_{AB} = \frac{ \sum\limits_{i=1}^n {Y_i.V_i}}{\sum\limits_{i=1}^n Y_i}$$- DÃĐterminer $V_a$ en fonction de $V_{froid}$ et $V_s$
- DÃĐterminer $V_b$ en fonction de $V_{chaud}$
- Exploitant le caractÃĻre linÃĐaire de l'amplificateur opÃĐrationnel, en dÃĐduire l'expression de $V_s$ en fonction de $V_e$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
, soit : $$$$ Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
, soit : $$$$ Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
, soit : $$$$ Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
- CaractÃĐristique entrÃĐe/sortie : approche complÃĻte
On prend maintenant en compte les capacitÃĐs $C$.
- Chercher la fonction de transfert de cet ÃĐtage d'entrÃĐe notÃĐe $H(p)=\frac{V_{s}}{V_{e}}$.
- Calculer la ou les frÃĐquences de coupures induites par les capacitÃĐs $C$.
- Tracer le diagramme de Bode asymptotique de ce montage.
Conseil : on pourra exprimer succÃĐssivement $V_a$ et $V_b$ comme prÃĐcÃĐdemment puis en dÃĐduire $V_s$ en fonction $V_e$.
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
, soit : $$$$ Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Yamaha Sound Processing
3. Etude du traitement YSP (Yamaha Sound Processing)
Le dernier circuit ÃĐtudiÃĐ rÃĐalise le traitement YSP (Yamaha Sound Processing) destinÃĐ aux enceintes de tÊte de la marque. Si ce nom flatteur semble cacher quelque chose de trÃĻs sophistiquÃĐ, la simple vue du schÃĐma montre qu'il n'en est rien; ce que confirme ÃĐvidemment l'ÃĐtude qui suit.
Le schÃĐma du circuit YSP est visible sur la figure ci-dessous :

L'entrÃĐe, notÃĐe $V_{e2}$, s'effectue sur la borne gauche de la capacitÃĐ C312. La sortie, notÃĐe $V_{s2}$, est situÃĐe à la sortie de IC303. A noter ÃĐgalement que le trait gras reprÃĐsente la ligne de masse.
Pour faciliter l'ÃĐtude, on exploitera le schÃĐma suivant, identique dans sa structure, mais utilisant des notations plus simples.

Dans toute la suite, on aborde les calculs dans le domaine de Laplace. Cela signifie qu'on utilisera l'impÃĐdance complexe gÃĐnÃĐralisÃĐe de la capacitÃĐ dans les calculs telle que $Z_c=\frac1{C.p}$. A noter qu'il sera parfois judicieux, en particulier en appliquant Millman, d'utiliser l'admittance de la capacitÃĐ $Y_c=C.p$.
- A l'aide du thÃĐorÃĻme de Millman, exprimer $V_a$ en fonction de $V_{s2}$, $V_{e2}$, $V_{b}$ et des diffÃĐrents composants.
- Exprimer $V_b$ en fonction de $V_a$, $R$ et $C$.
- Jugeant de la linÃĐaritÃĐ du circuit, exprimer $V_b$ en fonction $V_{s2}$.
- En dÃĐduire l'expression de la fonction de transfert du circuit ainsi rÃĐalisÃĐe $Hy(p)=\frac{V_{s2}}{V_{e2}}$
- DÃĐterminer l'expression de $\omega_0$ en fonction de $R1$, $R2$ et $C$.
- DÃĐterminer l'expression de $m$ en fonction de $R1$ et $R2$.
- Calculer numÃĐriquement la fÃĐquence libre liÃĐe à $\omega_0$ du filtre
- Calculer numÃĐriquement le coefficient d'amortissement du filtre
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Aide : on ÃĐcrira cette fonction de transfert sous la forme suivante : $Hy(p)=\frac{{p^2}/{{\omega_0}^2}}{1+2.m.{p}/{\omega_0}+{p^2}/{{\omega_0}^2}}$ oÃđ $m$ est le coefficient d'amortissement du filtre et $\omega_0$ sa pulsation libre.
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
MÊme si on reconnait aisÃĐment le type de filtre rÃĐalisÃĐ, l'expression reposant sur des composants n'est pas celle que l'on prÃĐvilÃĐgiera. Il convient donc maintenant d'exprimer les paramÃĻtres de rÃĐfÃĐrence que sont $m$ et $\omega_0$ de ce filtre en fonction des composants.
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Posez vos calculs intermédiaires ici et validez chacun d'entre eux en cliquant sur le bouton Ajouter l'ÃĐquation lorsque le champ d'ÃĐdition devient vert :
| , soit : | $$$$ |
Ajouter l'ÃĐquation ...
$$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Cliquer sur le bouton de la barre d'outils à droite pour saisir vos calculs. $$$$
Filtre à variables d'ÃĐtat
4. Etude du filtre à variables d'ÃĐtat (bloc State Variable Active Filter)
Dans cette partie, on ÃĐtudie le filtre active à variables d'ÃĐtats. Sa structure particuliÃĻre fournit plusieurs sorties (2 dans cet amplificateur) correspondant à diffÃĐrents type de filtre pour le mÊme signal d'entrÃĐe. L'amplificateur permet ensuite de sÃĐlectionner une des sorties pour cibler diffÃĐrentes sortes d'enceintes.
Le schÃĐma de cet ÃĐtage est le suivant :
On considÃĻre que les amplificateurs opÃĐrationnels fonctionnent tous en mode linÃĐaire.
On nÃĐglige les rÃĐsistances R317, R325, R341, R349 que l'on remplace par un court-circuit.
On remplace par un circuit ouvert les rÃĐsistance R336 et R345.Par commoditÃĐ, on note R1 = R315 = R318, P = VR301 = $100k\Omega$ , R2 = R321 , R3 = R323 = R329 = R334 , R = R338 = R347 , C = C314 = C316.
On dÃĐfinit ÃĐgalement les potentiels de sortie des amplificateurs opÃĐrationnels comme suit :
\(V_{a1}\) Ã la broche 1 de IC304 ,
\(V_{a2}\) Ã la broche 7 de IC304 ,
\(V_{a3}\) Ã la broche 1 de IC305,
\(V_{a4}\) Ã la broche 7 de IC304.
L'entrÃĐe, signal notÃĐ \(V_{ae}\), se fait sur la broche gauche de R315.
Les sorties sont notÃĐes \(V_{as1}=V_{a2}\) et \(V_{as2}=V_{a4}\).
- MÊme si on les nÃĐglige pour les calculs, quelle peut Être l'utilitÃĐ les rÃĐsistances R317, R325, R341, R349 ?
- Quelle est l'utilitÃĐ des rÃĐsistances R336 et R345 ?
- On dÃĐcompose l'ensemble du circuit en 4 :
- Partie 1 : circuit mettant en jeu le premier AOP
- DÃĐterminer \(V_{a1}=f_{1}\left(V_{ae},V_{a3}\right)\).
- Quelle type de fonction rÃĐalise cet AOP ? Par quel bloc peut-on le reprÃĐsenter ?
- Partie 2 : circuit mettant en jeu le second AOP
- DÃĐterminer \(V_{a2}=f_{2}\left(V_{a1},V_{a4}\right)\).
- Quelle type de fonction rÃĐalise cet AOP ? Par quel bloc peut-on le reprÃĐsenter ?
- Parties 3 et 4 (identiques) : circuit mettant en jeu le 3 iÃĻme AOP ou le 4 iÃĻme.
- DÃĐterminer \(V_{a3}=f_{3}\left(V_{a2}\right)\)
- Quelle fonction rÃĐalise cet AOP ? Par quel bloc peut-on le reprÃĐsenter ?
- Partie 1 : circuit mettant en jeu le premier AOP
- ReprÃĐsenter le schÃĐma bloc complet du circuit (en reprenant le blocs obtenus à la question prÃĐcÃĐdente).
- Etude du traitement obtenu sur la sortie \(V_{a2}\).
- DÃĐterminer la fonction de transfert \(H_{a1}\left(p\right)=\frac{V_{a2}}{V_{ae}}\)
- Quels sont les grandeurs caractÃĐristiques de cette fonction de transfert.
- ReprÃĐsenter son diagramme de Bode asymptotique en se limitant au gain.
- Quel traitement obtient-on sur cette sortie ?
- A quel type d'enceinte correspond ce traitement ?
- Reprendre les questions prÃĐcÃĐdentes pour la sortie \(V_{a4}\) avec l'ÃĐtude de la fonction de transfert \(H_{a2}\left(p\right)=\frac{V_{a4}}{V_{ae}}\).